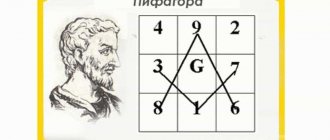
Магический квадрат Пифагора, или, как его ещё называют, психосоматрица, придуман легендарным древнегреческим учёным и является ключевым понятием в нумерологии. С расчёта квадрата Пифагора начинается анализ личностных качеств человека.
По вашим просьбам мы подготовили приложение «Нумерология» для смартфона.
Приложение умеет ежедневно присылать Ваше Персональное Число Дня. В нем мы собрали важнейшие нумерологические расчеты с подробной расшифровкой.
Скачайте бесплатно:
Он определяет силу характера и энергетики, слабые места здоровья, развитость интеллекта и прочие личностные качества, которые даны человеку судьбой от рождения.
Определение магического квадрата
Магический квадрат — это квадратная — таблица целых чисел от 1 до , удовлетворяющая следующим условиям:
, (1)
где
Простыми словами магический квадрат — это квадратная матрица (таблица) чисел, сумма который по вертикали, горизонтали и диагонали равна одному и тому же числу.
Вычисления с помощью NVIDIA CUDA
Если не вдаваться в подробности, то процесс вычислений, выполняющийся на видеокарте, можно представить как несколько параллельных аппаратных блоков (blocks), каждый из которых выполняет несколько процессов (threads).
Для примера можно привести пример функции сложения 2х векторов из документации CUDA:
__global__ void add(int n, float *x, float *y) { int index = threadIdx.x; int stride = blockDim.x; for (int i = index; i < n; i += stride) y
= x + y; } Массивы x и y — общие для всех блоков, а сама функция таким образом выполняется одновременно сразу на нескольких процессорах. Ключ тут в параллелизме — процессоры видеокарты гораздо проще чем обычный CPU, зато их много и они ориентированы именно на обработку числовых данных.
Это то, что нам нужно. Мы имеем матрицу чисел X11, X12,..,X44. Запустим процесс из 16 блоков, каждый из которых будет выполнять 16 процессов. Номеру блока будет соответствовать число X11, номеру процесса число X12, а сам код будет вычислять все возможные квадраты с для выбранных X11 и X12. Все просто, но здесь есть одна тонкость — данные нужно не только вычислить, но и передать с видеокарты обратно, для этого в нулевом элементе массива будем хранить число найденных квадратов.
Основной код получается весьма простым:
#define N 4 #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) int main(int argc,char *argv[]) { const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p Мы выделяем блок памяти на видеокарте с помощью cudaMalloc, запускаем функцию squares, указав ей 2 параметра 16,16 (число блоков и число потоков), соответствующие перебираемым числам 1..16, затем копируем данные обратно через cudaMemcpy.
Сама функция squares по сути повторяет код из предыдущей части, с той разницей, что приращение количества найденных квадратов делается с помощью atomicAdd — это гарантирует что переменная будет корректно изменяться при одновременных обращениях.
Исходный код целиком
// Compile: // nvcc -o magic4_gpu.exe magic4_gpu.cu #include #include #define N 4 #define MAX (N*N) #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) #define S 34 // Magic square: // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 __global__ void squares(int *res_array) { int index1 = blockIdx.x, index2 = threadIdx.x; if (index1 + 1 > MAX || index2 + 1 > MAX) return; const int x11 = index1+1, x12 = index2+1; for(int x13=1; x13<=MAX; x13++) { if (x13 == x11 || x13 == x12) continue; int x14 = S — x11 — x12 — x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; for(int x21=1; x21<=MAX; x21++) { if (x21 == x11 || x21 == x12 || x21 == x13 || x21 == x14) continue; for(int x22=1; x22<=MAX; x22++) { if (x22 == x11 || x22 == x12 || x22 == x13 || x22 == x14 || x22 == x21) continue; for(int x23=1; x23<=MAX; x23++) { int x24 = S — x21 — x22 — x23; if (x24 < 1 || x24 > MAX) continue; if (x23 == x11 || x23 == x12 || x23 == x13 || x23 == x14 || x23 == x21 || x23 == x22) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; for(int x31=1; x31<=MAX; x31++) { if (x31 == x11 || x31 == x12 || x31 == x13 || x31 == x14 || x31 == x21 || x31 == x22 || x31 == x23 || x31 == x24) continue; for(int x32=1; x32<=MAX; x32++) { if (x32 == x11 || x32 == x12 || x32 == x13 || x32 == x14 || x32 == x21 || x32 == x22 || x32 == x23 || x32 == x24 || x32 == x31) continue; for(int x33=1; x33<=MAX; x33++) { int x34 = S — x31 — x32 — x33; if (x34 < 1 || x34 > MAX) continue; if (x33 == x11 || x33 == x12 || x33 == x13 || x33 == x14 || x33 == x21 || x33 == x22 || x33 == x23 || x33 == x24 || x33 == x31 || x33 == x32) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; const int x41 = S — x11 — x21 — x31, x42 = S — x12 — x22 — x32, x43 = S — x13 — x23 — x33, x44 = S — x14 — x24 — x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x44 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; // Square found: save in array (MAX numbers for each square) int p = atomicAdd(res_array, 1); if (p >= SQ_MAX) continue; int i = MAX*p + 1; res_array
= x11; res_array[i+1] = x12; res_array[i+2] = x13; res_array[i+3] = x14; res_array[i+4] = x21; res_array[i+5] = x22; res_array[i+6] = x23; res_array[i+7] = x24; res_array[i+8] = x31; res_array[i+9] = x32; res_array[i+10] = x33; res_array[i+11] = x34; res_array[i+12]= x41; res_array[i+13]= x42; res_array[i+14] = x43; res_array[i+15] = x44; // Warning: printf from kernel makes calculation 2-3x slower // printf(«%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n», x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); } } } } } } } } int main(int argc,char *argv[]) { int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p
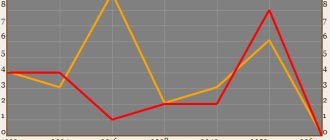
Результат не требует комментариев — время выполнения составило
2.7с
, что примерно в 30 раз лучше изначального однопоточного варианта:
Как подсказали в комментариях, можно задействовать еще больше аппаратных блоков видеокарты, так что был испробован вариант из 256 блоков. Изменение кода минимально:
__global__ void squares(int *res_array) { int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX; … } squares<<>>(gpu_out); Это сократило время еще в 2 раза, до
1.2с
. Далее, на каждом блоке можно запустить 16 процессов, что дает наилучшее время
0.44с
.
Окончательный вариант кода
#include #include #define N 4 #define MAX (N*N) #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) #define S 34 // Magic square: // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 __global__ void squares(int *res_array) { int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX, index3 = threadIdx.x; if (index1 + 1 > MAX || index2 + 1 > MAX || index3 + 1 > MAX) return; const int x11 = index1+1, x12 = index2+1, x13 = index3+1; if (x13 == x11 || x13 == x12) return; int x14 = S — x11 — x12 — x13; if (x14 < 1 || x14 > MAX) return; if (x14 == x11 || x14 == x12 || x14 == x13) return; for(int x21=1; x21<=MAX; x21++) { if (x21 == x11 || x21 == x12 || x21 == x13 || x21 == x14) continue; for(int x22=1; x22<=MAX; x22++) { if (x22 == x11 || x22 == x12 || x22 == x13 || x22 == x14 || x22 == x21) continue; for(int x23=1; x23<=MAX; x23++) { int x24 = S — x21 — x22 — x23; if (x24 < 1 || x24 > MAX) continue; if (x23 == x11 || x23 == x12 || x23 == x13 || x23 == x14 || x23 == x21 || x23 == x22) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; for(int x31=1; x31<=MAX; x31++) { if (x31 == x11 || x31 == x12 || x31 == x13 || x31 == x14 || x31 == x21 || x31 == x22 || x31 == x23 || x31 == x24) continue; for(int x32=1; x32<=MAX; x32++) { if (x32 == x11 || x32 == x12 || x32 == x13 || x32 == x14 || x32 == x21 || x32 == x22 || x32 == x23 || x32 == x24 || x32 == x31) continue; for(int x33=1; x33<=MAX; x33++) { int x34 = S — x31 — x32 — x33; if (x34 < 1 || x34 > MAX) continue; if (x33 == x11 || x33 == x12 || x33 == x13 || x33 == x14 || x33 == x21 || x33 == x22 || x33 == x23 || x33 == x24 || x33 == x31 || x33 == x32) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; const int x41 = S — x11 — x21 — x31, x42 = S — x12 — x22 — x32, x43 = S — x13 — x23 — x33, x44 = S — x14 — x24 — x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x44 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; // Square found: save in array (MAX numbers for each square) int p = atomicAdd(res_array, 1); if (p >= SQ_MAX) continue; int i = MAX*p + 1; res_array
= x11; res_array[i+1] = x12; res_array[i+2] = x13; res_array[i+3] = x14; res_array[i+4] = x21; res_array[i+5] = x22; res_array[i+6] = x23; res_array[i+7] = x24; res_array[i+8] = x31; res_array[i+9] = x32; res_array[i+10] = x33; res_array[i+11] = x34; res_array[i+12]= x41; res_array[i+13]= x42; res_array[i+14] = x43; res_array[i+15] = x44; // Warning: printf from kernel makes calculation 2-3x slower // printf(«%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n», x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); } } } } } } } int main(int argc,char *argv[]) { int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p
Скорее всего, это далеко не идеал, например можно запустить еще больше блоков на GPU, но это сделает код более запутанным и сложным для понимания. И разумеется, расчеты даются не «бесплатно» — при загруженном GPU интерфейс Windows начинает заметно подтормаживать, а энергопотребление компьютера увеличивается практически в 2 раза, с 65 до 130Вт.
Правка
: как подсказал в комментариях пользователь Bodigrim, для квадрата 4х4 выполняется еще одно равенство: сумма 4х «внутренних» ячеек равна сумме «внешних», она же равна S.
X22 + X23 + X32 + X33 = X11 + X41 + X14 + X44 = S
Это позволит еще ускорить алгоритм, выразив одни переменные через другие и убрав еще 1-2 вложенных цикла, обновленный вариант кода можно найти в комментарии ниже.
Древние магические квадраты
Однако, расстановка чисел в магическом квадрате не обязательно будет однозначной. Например, посмотрите два магических квадрата размером :
Первый магический квадрат:
| 7 | 12 | 1 | 14 |
| 2 | 13 | 8 | 11 |
| 16 | 3 | 10 | 5 |
| 9 | 6 | 15 | 4 |
Этот квадрат был впервые найден в Индии, и трактовался, как дьявольский квадрат, датируется 11 веком. В действительности очень интересно узнать, откуда люди решили, что искомая сумма числе по строке, по столбцу или по диагонали должна быть именно 34?
А вот еще один магический квадрат размера . Этот квадрат уже из 16 века. Этот квадрат был обнаружен на гравюре, которую создал Альберт Дюрер и назвал ее «Меланхолия I». Поэтому квадрат называют «магический квадрат Дюрера». Гравюра была написана в 1514 году и три числа внизу указывают год ее создания.
Известно более 48 видов магических квадратов размера .
Как гадать?
Это гадание можно использовать всегда и везде, и применять его в разных случаях и непростых жизненных ситуациях. Основа предсказания – квадрат, расчерченный на клетки.
Внутри такой таблицы вписаны слова в разном порядке, самые случайные. Они-то и указывают на то, что будет. Чтобы погадать, нужно подумать о том вопросе, который волнует, и рассеянным, расфокусированным взглядом посмотреть на таблицу. Взгляд сам «выхватит» из таблицы три слова, одно за другим. Они-то и будут ответом!
Просто посмотрите на таблицу и «выловите» три слова, которые расскажут о вашем характере и особенностях, а также – о ближайшем будущем.
Минимально возможные суммы магического квадрата
Постоянные значения M суммы магических квадратов имеют минимальное значение (для положительных ненулевых целочисленных значений):
Для размера 3×3 минимальная сумма равна 15, для 4×4 — 34, для 5×5 — 65, для 6×6 — 111, затем 175, 260, …
Все, что меньше, вынуждает использовать отрицательные числа или дроби (не целые числа) для решения магического квадрата.
Магический квадрат Франклина восьмого порядка
Квадрат Франклина — это панмагический квадрат с магической постоянной 260. Интересный квадрат с множеством свойств. Рекомендую прочитать статью о нем: https://klassikpoez.narod.ru/franklin.htm
| 52 | 61 | 4 | 13 | 20 | 29 | 36 | 45 |
| 14 | 3 | 62 | 51 | 46 | 35 | 30 | 19 |
| 53 | 60 | 5 | 12 | 21 | 28 | 37 | 44 |
| 11 | 6 | 59 | 54 | 43 | 38 | 27 | 22 |
| 55 | 58 | 7 | 10 | 23 | 26 | 39 | 42 |
| 9 | 8 | 57 | 56 | 41 | 40 | 25 | 24 |
| 50 | 63 | 2 | 15 | 18 | 31 | 34 | 47 |
| 16 | 1 | 64 | 49 | 48 | 33 | 32 | 17 |
Бимагические и тримагические квадраты
Бимагическим квадратом называется квадрат, который остается магическим тогда, когда мы заменяем все его числа квадратами этих чисел.
Паскаль написал небольшой трактат и би- и три- магических квадратах.
Тримагическим квадратом называется квадрат, который остается магическим тогда, когда мы заменяем все его числа кубами этих чисел.
Бимагические квадрат размером 128 x 128 был обнаружен в 1905 году. В 2002 году, немцу Уолтеру Трампу удалось построить тримагический квадрат 12 x 12 и это минимальное измерение, которое возможно для этого вида магического квадрата.
LiveInternetLiveInternet
—Музыка
—Метки
—Рубрики
—Цитатник
. Года два назад многие блоггеры были возмущены наглым копипастом и писали посты на тему борьбы с н.
Посетите музеи онлайн В связи с отменой культурно-массовых мероприятий появилась возможно.
Упражнения для глаз, чтобы остановить падение зрения Хотите остановить падение зрения, снизить.